推荐学习书目
› Learn Python the Hard Way
Python Sites
› PyPI - Python Package Index
› http://diveintopython.org/toc/index.html
› Pocoo
值得关注的项目
› PyPy
› Celery
› Jinja2
› Read the Docs
› gevent
› pyenv
› virtualenv
› Stackless Python
› Beautiful Soup
› 结巴中文分词
› Green Unicorn
› Sentry
› Shovel
› Pyflakes
› pytest
Python 编程
› pep8 Checker
Styles
› PEP 8
› Google Python Style Guide
› Code Style from The Hitchhiker's Guide
V2EX › Python
大盘的频域分析--高低频信号处理(利用 matlab 分析而得出,不构成任何投资建议)
datayes2015 · 2016-10-19 18:21:11 +08:00 · 3176 次点击这是一个创建于 3291 天前的主题,其中的信息可能已经有所发展或是发生改变。
人类对于股市波动规律的认知,是一个极具挑战性的世界级难题。迄今为止,尚没有任何一种理论和方法能够令人信服并且经得起时间检验—— 2000 年,著名经济学家罗伯特·席勒在《非理性繁荣》一书中指出:“我们应当牢记,股市定价并未形成一门完美的科学”; 2013 年,瑞典皇家科学院在授予罗伯特·席勒等人该年度诺贝尔经济学奖时指出:几乎没什么方法能准确预测未来几天或几周股市债市的走向,但也许可以通过研究对三年以上的价格进行预测。美国证券分析家拉尔夫·.纳尔逊·.艾略特( IiR.N.Elliott )根据这一发现他提出了一套相关的市场分析理论,精炼出市场的 13 种形态( Patte·rn )或波浪( Waves ),在市场上这些型态重复出现,但是出现的时间间隔及幅度大小并不一定具有再现性。而后他又发现了这些呈结构性型态之图形可以连接起来形成同样型态的更大图形。这样提出了一系列权威性的演绎法则用来解释市场的行为,并特别强调波动原理的预测价值,这就是久负盛名的艾略特波浪理论。艾略特波浪理论( Elliott Wave Theory )是股票技术分析的一种理论。认为市场走势不断重复一种模式,每一周期由 5 个上升浪和 3 个下跌浪组成。艾略特波浪理论将不同规模的趋势分成九大类,最长的超大循环波(grand supercycle) 是横跨 200 年的超大型周期,而次微波(subminuette)则只覆盖数小时之内的走势。但无论趋势的规模如何,每一周期由 8 个波浪构成这一点是不变的。
任何函数都可以在频域空间上进行展开,用以分析其周期特性。对此,我们不妨先做个大胆的假设,假设大盘具有某些不为人知的周期性质(波浪理论)。如果,我们能够弄清大盘的周期特性,那将会使得我们对大盘的起伏具有更深刻的认识。
f(t)是 t 的周期函数,如果 t 满足狄里赫莱条件:在一个以 2T 为周期内 f(X)连续或只有有限个第一类间断点,附 f ( x )单调或可划分成有限个单调区间,则 F ( x )以 2T 为周期的傅里叶级数收敛,和函数 S ( x )也是以 2T 为周期的周期函数,且在这些间断点上,函数是有限值;在一个周期内具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算 f(t)的傅立叶变换,
②式的积分运算叫做 F(ω)的傅立叶逆变换。 F(ω)叫做 f(t)的像函数, f(t)叫做
F(ω)的像原函数。 F(ω)是 f(t)的像。 f(t)是 F(ω)原像。
公式: https://uqer.io/community/share/57e8aaa6228e5b47ec0d8ee1
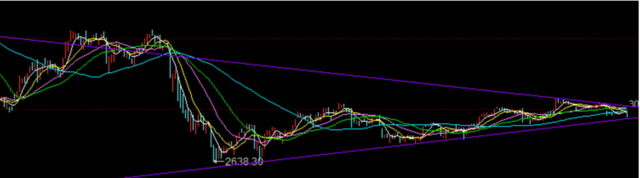
现在,我们取出每天的涨跌幅,重新得到涨跌幅随时间的变化( 365 天)
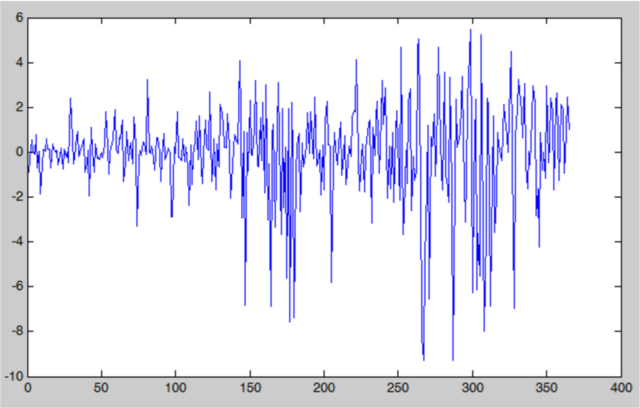
由于考虑到越近的股价波动对今后的股价影响越大,故对其权重按照指数衰减的方式重新调整。
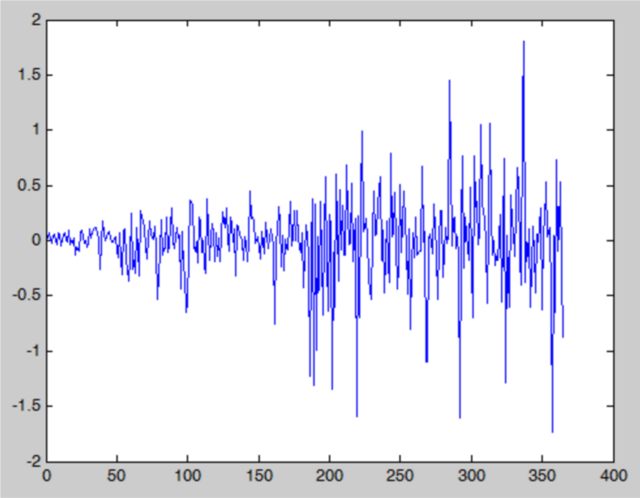
然后,我们便可以对其做傅立叶变换( FFT ),得到这组震荡函数在频域上的分布:
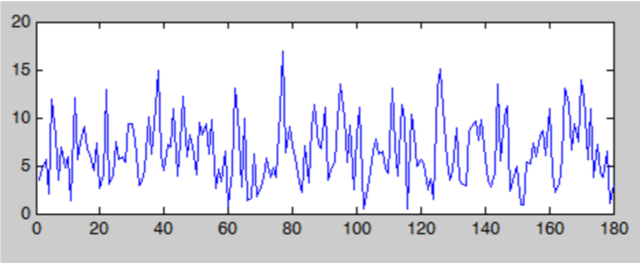
由于,在频域上出现高频和低频信号的幅度几乎都是差不多,而且没有明显的峰值。但是在某些特定日期的周期上存在相对强的振幅。为了能够预测一两周的大致走势,所以,我们去掉了低频( 1 天的震荡)和高频的分量(一年的震荡)。然后采用傅立叶逆变换来还原之前的函数。所以原函数和还原后的函数有略微的差异。
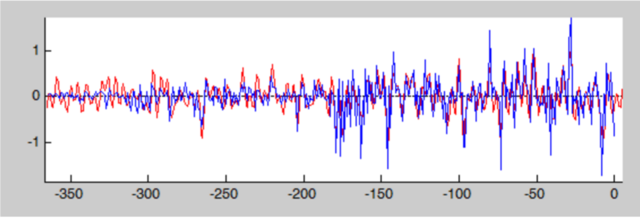
最后,我们利用还原后的函数得到未来大致的涨跌幅(红色曲线超出蓝色曲线的部分)。
利用涨跌幅再进一步还原往后的股价走势
图片: https://uqer.io/community/share/57e8aaa6228e5b47ec0d8ee1
可以看到,通过频域信号的处理,我们滤过了高频和低频的信号,而只重视以大概一周为周期的股价波动的周期信号来还原股价的波动性。包含了股价处于不同波段的位置(波峰或波谷),从而预测股票的价格。
从结果上看,为了几天内可能还会出现振荡走低的结构,但随和会出现一波反弹。
以上结构都是利用 matlab 分析而得出,不构成任何投资建议,只是提供一种思路供大家交流学习。
任何函数都可以在频域空间上进行展开,用以分析其周期特性。对此,我们不妨先做个大胆的假设,假设大盘具有某些不为人知的周期性质(波浪理论)。如果,我们能够弄清大盘的周期特性,那将会使得我们对大盘的起伏具有更深刻的认识。
f(t)是 t 的周期函数,如果 t 满足狄里赫莱条件:在一个以 2T 为周期内 f(X)连续或只有有限个第一类间断点,附 f ( x )单调或可划分成有限个单调区间,则 F ( x )以 2T 为周期的傅里叶级数收敛,和函数 S ( x )也是以 2T 为周期的周期函数,且在这些间断点上,函数是有限值;在一个周期内具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算 f(t)的傅立叶变换,
②式的积分运算叫做 F(ω)的傅立叶逆变换。 F(ω)叫做 f(t)的像函数, f(t)叫做
F(ω)的像原函数。 F(ω)是 f(t)的像。 f(t)是 F(ω)原像。
公式: https://uqer.io/community/share/57e8aaa6228e5b47ec0d8ee1

现在,我们取出每天的涨跌幅,重新得到涨跌幅随时间的变化( 365 天)

由于考虑到越近的股价波动对今后的股价影响越大,故对其权重按照指数衰减的方式重新调整。

然后,我们便可以对其做傅立叶变换( FFT ),得到这组震荡函数在频域上的分布:

由于,在频域上出现高频和低频信号的幅度几乎都是差不多,而且没有明显的峰值。但是在某些特定日期的周期上存在相对强的振幅。为了能够预测一两周的大致走势,所以,我们去掉了低频( 1 天的震荡)和高频的分量(一年的震荡)。然后采用傅立叶逆变换来还原之前的函数。所以原函数和还原后的函数有略微的差异。

最后,我们利用还原后的函数得到未来大致的涨跌幅(红色曲线超出蓝色曲线的部分)。
利用涨跌幅再进一步还原往后的股价走势
图片: https://uqer.io/community/share/57e8aaa6228e5b47ec0d8ee1
可以看到,通过频域信号的处理,我们滤过了高频和低频的信号,而只重视以大概一周为周期的股价波动的周期信号来还原股价的波动性。包含了股价处于不同波段的位置(波峰或波谷),从而预测股票的价格。
从结果上看,为了几天内可能还会出现振荡走低的结构,但随和会出现一波反弹。
以上结构都是利用 matlab 分析而得出,不构成任何投资建议,只是提供一种思路供大家交流学习。
1
grindsgears 2016-10-19 18:43:16 +08:00 via iPhone
。。。。
今天忍不住要多说几句 难道你不知道 implied 波动 现在有 ivix 和 cvx 。 lol |
2
Borden 2016-10-19 19:02:15 +08:00
这类数据分析浩如烟海,不客气地说,楼主这个一分钱价值都没有。
|
3
JackBlack2006 2016-10-19 19:32:50 +08:00
半夜放个政策,第二天开盘涨停或者跌停,能分析出来么。
还不如内部消息 |
4
lllang 2016-10-19 21:21:57 +08:00
最后一句话白加了,大家并不相信你。哈哈
|