上篇文章介绍了 TiDB 如何使用 Jepsen 来进行一致性验证,并且介绍了具体的测试案例,但是并没有对 Jepsen 背后的一致性验证算法做过多介绍。这篇文章将会深入 Jepsen 的核心库 knossos,介绍 knossos 库所涉及的 Linearizability (线性化)一致性验证算法。
Linearizability 一致性模型
什么是一致性模型?
一致性模型确定了编写系统的程序员与系统之间的某种协议,如果程序员遵守了这种协议,那么这个系统就能提供某种一致性。常见的一致性模型有:
- Strict Consistency
- Linearizability (Atomic Consistency)
- Sequential Consistency
- Casual Consistency
- Serializability
- ……
需要注意的是这里的系统指并发系统,分布式系统只是其中的一类。
什么是 Linearizability ?
首先我们需要引入历史( history )的概念,历史是并发系统中由 invocation 事件和 response 事件组成的有限序列。
invocation: <x op(args*) A>,x 表示被执行对象的名称; op 表示操作名称,如读和写; args* 表示一系列参数值; A 表示进程的名称
response:<x term(res*) A>,term 表示结束( termination )状态; res* 表示一系列结果值
如果 invocation 和 response 的 x (对象)和 A (进程)相同,那么我们认为它们是对应操作,并且 complete ( H )表示历史中的最多成对操作
当我们的历史 H 满足以下条件时我们把它称为顺序化( sequential )历史:
- H 中的第一个事件是 invocation
- 除了可能的最后一个事件外,每个 invocation 事件都紧跟着对应[^对应意味着对象和进程相同]的 response 事件;每个 response 事件都紧跟着对应的 invocation 事件
H|A 代表只含有进程 A 操作的子历史,H|x 代表只含有对象 x 操作的子历史
定义 well-formed:如果每个进程子历史 H|A 都是顺序化的,那么这个历史 H 就是 well-formed。
如果一个历史不是顺序化的话那么就是并发的。
历史 H 在操作上引出非自反的偏序关系$<_H$
$e_0 <_H e_1$ if $res(e_0)$ precedes $inv(e_1)$ in $H$
这里的 res 和 inv 分别对应 response 和 invocation。
当历史 H 可以通过增加>=0 个 response 事件被延长时成为 H' 并且满足以下两个条件时,则这个历史是线性化( linearizable )的。
L1: complete(H') 与某个合法的顺序化历史 S 相等
L2: $<_H ⊆ <_S$
complete(H')表示进程以完整的操作进行交互,L2 表示如果 op1 在 H 中先于 op2 存在(注意这里的先于强调实时发生的顺序 real-time order ),那么在 S 中也是这样。我们把 S 称为 H 的线性化点( linearization )。
下面我们通过 3 个小例子来解释一下以上 2 个条件。
q 代表 FIFO 队列,A、B 代表两个进程
q Enq(x) A
q Deq() B
q Ok(x) B
满足 linearizable,虽然 Enq(x)并没有返回 Ok,但是我们可以通过增加这条返回语句使得上述语句与某个合法的顺序化历史相等
q Enq(x) A
q Ok() A
q Enq(y) B
q Ok() B
q Deq() A
q Ok(y) A
如果满足 linearizable 那必然 Enq(x)先于 Enq(y),但是 Deq()是得到的却是 y,所以违反了 L2,因此这段历史不是线性化的
q Enq(y) A
q Ok() A
q Deq() A
q Deq() B
q Ok(y) A
q Ok(y) B
不满足 linearizable 因为 Enq(y)只执行了一次,却被 Deq()了两次,不能与任何合法的顺序化历史相对应
Linearizability 的性质
- 局部性( Locality ),当且仅当 H 中每个对象 x 都是线性化的,才能保证 H 是线性化的
- 非阻塞( Nonblocking ),invocation 事件不用等待对应的 response 事件
验证 Linearizability
正确( correctness )的定义
一段历史 H 由两种对象组成,representation(REP)和 abstract(ABS)。abstract 是被实现的类型,而 representation 类型则是用于实现 ABS 的类型。这两种对象在以下条件下进行交互:
- 子历史 H|REP 和 H|ABS 是 well-formed
- 对于每个进程 P,在子历史 H|P 中,每一个 rep 操作都被 abs 操作所包含
对于某个实现中的所有历史 H 来说,如果 H|ABS 是线性化的,那么这个实现就是正确的。
REP 值的子集中的合法表现由表达不变性( representation invariant )所表示:I: REP-> BOOL,一个合法表现的含义由抽象函数( abstract function )所表示:A: REP->ABS。对于一个正确的实现 p 来说,存在一个表达不变性 I,以及一个抽象函数 A,并且无论何时 p 从一个合法的表达值 r 到达另一个表达值 r',抽象操作 a 把抽象值 A(r)变成 A(r')。
我们从最简单的队列( FIFO queue )入手。
struct queue {
int back;
element *elements;
};
bool Enq(queue *q, element x)
{
int i = INC(&q->back); // 原子自增并返回之前的值
STORE(&q->elements[i], x); // 假设内存足够
return true;
}
element Deq(queue *q)
{
while (1) {
int end = READ(&q->back); // 原子读取
for (int i = 1; i < end; ++i) {
element x = CAS(&q->elements[i], NULL); // 返回 CAS 之前的值
if (x != NULL) return x;
}
}
}
Enq 和 Deq 可以看做是 abstract operation,而 Enq 和 Deq 中的每条语句可以看做是 representation operation。
对线性化的历史的验证可以被转换为对顺序化历史的验证,对于给定的线性化历史,我们把最终线性化点的对象的值称为线性值。因为给定的历史可能有超过一个线性化点,所以这个对象可能会有多个线性值。我们用 Lin(H) 表示所有线性值的集合,可以把它们看作是系统外部的观察者所看到的值。
对于以下几个队列操作,对应的线性值分别有以下几种。
| History | Linearized values | | :------: | :--------------------------: | | \ | {[]} | | Enq(x) A | {[], [x]} | | Enq(y) B | {[], [x], [y], [x,y], [y,x]} | | Ok() B | {[y], [x,y], [y,x]} | | Ok() A | {[x,y], [y,x]} | | Deq() C | {[x], [y], [x,y], [y,x]} | | Ok(x) C | {[y]} |
为了证明正确性,我们需要保证:
For all $r$ in $Lin(H|REP)$, $I(r)$ holds and $A(r) ⊆ Lin(H|ABS)$
其中 H|REP 和 H|ABS 都是线性化的,r 代表 H|REP 的线性值,并且
$I(r) = (r.back ≥ 1)$ & $(∀ i. i ≥ r.back -> r.elements[i] = null)$ & $(lbound(r.elements) = 1)$
其中 lbound 是最小的数组索引(队列从 1 开始)
$A(r)$ = {$q | elements(r) = elements(q)$ & $<_r ⊆ <_q$}
其中偏序关系$<_r$表示如果被插入元素 x 的赋值操作先于 y 的自增操作,则 $x <_r y,<_q$ 代表队列 q 的全序关系。
换句话说,队列的表现值( representation value )就是队列中的元素,这些元素的排列顺序与 Enq 操作的顺序一致。
下面这张图可以帮助你很好地理解上述公式的意思。第二列是线性化的表现值( linearized representation values ),第三列是线性化的抽象值( linearized abstract values ),可以看到每一行中第二列都是第三列的子集。

Wing & Gong 线性化算法
介绍完了如何证明 linearizability,下面我们可以继续深入到 knossos 使用的两个核心算法之一—— Wing & Gong Linearibility 算法( WGL )。
WGL 算法:对于给定的某个数据类型 T,它的并发实现为 ConcObj,而它的顺序化要求为 SeqObj。对于给定的历史 H,我们在保证 H 的实时顺序 $<_H$ 的情况下尝试 H 的每一系列可能的顺序化操作,然后检查每个顺序化历史 $H_S$ 在 SeqObj 上执行时是否是线性化的。如果 H 的每一种可能都失败了,那么这个历史就不是线性化的。
我们定义历史是由一系列事件组成的:
typedef struct ev {
char item;
char op;
struct ev *match, *prev, *next;
} event;
其中 iterm 是操作 op 的参数,name 是进行操作的进程的名字,prev 和 next 分别表示上一个和下一个事件,match 指向其对应的返回( res )事件。
另外我们还需要区域以及 lift(unlift)这个概念。
区域( Section ):由触发( inv )事件,对应的返回事件,以及它们中间包含的所有事件。
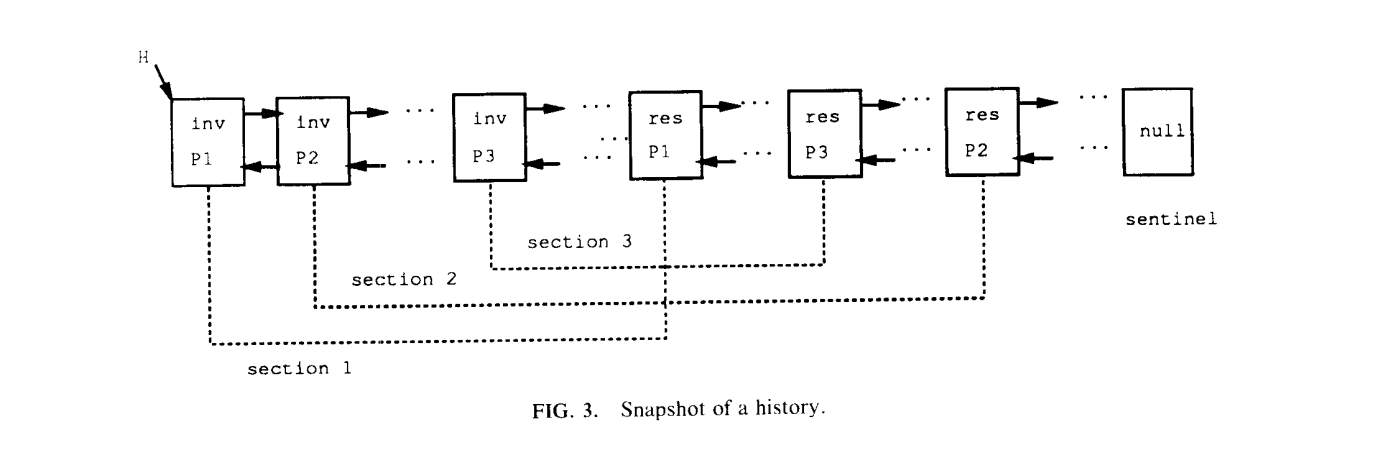
虚线同时可以看作是也是 match 指针。
lift:将某对操作从历史中移出
unlift:将移出的某对操作放回

这个算法的核心是一个搜索( Search )函数,如果历史 H 是线性化的,那么那么他返回一个线性化点(即顺序化历史 S )。搜索使用一个栈来保存历史中已经线性化的部分,这个栈及栈中的元素是这样定义的:
typedef struct {
event *pi, *pr, *inv, *resp;
char item, op, result;
} elt_stack;
typedef struct {
elt_stack value[STACK_LENGTH];
int in;
} stacktype;
其中 pi 和 pr 分别表示子历史中第一个没有被检查的区域; inv 和 resp 表示子历史中第一对操作; item、op 和 result 记录这对操作的信息。
一个完整的搜索函数是这样的:
-
初始化栈
-
通过 current 操作的 pi 和 pr 定位当前的区域,否则返回线性化点
-
从当前区域开始,选择一个操作并且将它的信息存储在 current 中
-
对选择的操作进行顺序化模拟,调用 op
- A:如果 op 返回真,意味着目前被检查的所有操作能够组成线性化的子历史,所以把这个操作推入栈中,并将这个操作从历史中移出,然后回到 2
- B: ① 如果当前区域内还有一些未被选择的触发( inv )事件没有排在任何返回( res )事件之后,那么选择一个然后回到 4 ;② 当前区域的所有操作已经被尝试但是失败了,所以我们需要将操作出栈然后尝试其他的顺序,如果栈是空的,那么意味着历史不是线性化的,函数返回;否则,将顶层元素出栈,这个元素包含了之前区域的所有信息,以及被选择的操作,然后 undo 之前的 op,unlift 这个操作,最后,设置 current 为之前区域的指针,然后回到 5B①
注:4 中 op 操作取决于具体模型,如果被测试的是一个寄存器的话,那 op 可以是 read、write 和 cas,如果 read 和 cas 时读到的值和预期值不一致,则操作无法进行。
这就是整个 WGL 算法。这个算法很简单也很好理解,但是有两个明显的缺点:
- 一旦操作数量上升,整个算法会运行地很缓慢,因为可能会出现涉及大量回溯的操作
- 这个算法只能验证是否线性化,一旦线性化不成立,并不能给出具体违反线性化的出错点
对此 knossos 库的第二个算法使用了 WGL 算法的改进版本,与 WGL 中的栈存放操作信息不同的是它使用了树遍历和图搜索两种方法来使算法更高效,同时存在“记忆”机制来避免对相同的操作进行重复验证,并且如果所验证的历史不满足一致性,会给出具体出错的点。篇幅有限,如果你对这个算法感兴趣的话,文末有链接。
最后的思考
这篇文章介绍了什么是 Linearizability、Linearizability 正确性的验证及其算法。这些算法在分布式系统中的应用只是一个很小的方面,算法本身是独立的,它只需要一个历史 H,至于这个历史是随机生成的还是某个应用在实际中产生的并不重要。你可以使用这些算法对任何并发系统进行验证,小到一个无锁队列、Set,大到某个分布式系统。TiDB 作为一个分布式数据库却能被抽象化为一个队列、寄存器来被用作测试这本身就是一个很有意思的地方,同时也很好地展现了这些算法自身的魅力。
参考
Linearizability versus Serializability
徐鹏